Continuous

Uniform(name, *args, **kwargs)	Continuous uniform log-likelihood.
Flat(name, *args, **kwargs)	Uninformative log-likelihood that returns 0 regardless of the passed value.
HalfFlat(name, *args, **kwargs)	Improper flat prior over the positive reals.
Normal(name, *args, **kwargs)	Univariate normal log-likelihood.
TruncatedNormal(name, *args, **kwargs)	Univariate truncated normal log-likelihood.
HalfNormal(name, *args, **kwargs)	Half-normal log-likelihood.
SkewNormal(name, *args, **kwargs)	Univariate skew-normal log-likelihood.
Beta(name, *args, **kwargs)	Beta log-likelihood.
Kumaraswamy(name, *args, **kwargs)	Kumaraswamy log-likelihood.
Exponential(name, *args, **kwargs)	Exponential log-likelihood.
Laplace(name, *args, **kwargs)	Laplace log-likelihood.
AsymmetricLaplace(name, *args, **kwargs)	Asymmetric-Laplace log-likelihood.
StudentT(name, *args, **kwargs)	Student’s T log-likelihood.
HalfStudentT(name, *args, **kwargs)	Half Student’s T log-likelihood
Cauchy(name, *args, **kwargs)	Cauchy log-likelihood.
HalfCauchy(name, *args, **kwargs)	Half-Cauchy log-likelihood.
Gamma(name, *args, **kwargs)	Gamma log-likelihood.
InverseGamma(name, *args, **kwargs)	Inverse gamma log-likelihood, the reciprocal of the gamma distribution.
Weibull(name, *args, **kwargs)	Weibull log-likelihood.
Lognormal(name, *args, **kwargs)	Log-normal log-likelihood.
ChiSquared(name, *args, **kwargs)	\(\chi^2\) log-likelihood.
Wald(name, *args, **kwargs)	Wald log-likelihood.
Pareto(name, *args, **kwargs)	Pareto log-likelihood.
ExGaussian(name, *args, **kwargs)	Exponentially modified Gaussian log-likelihood.
VonMises(name, *args, **kwargs)	Univariate VonMises log-likelihood.
Triangular(name, *args, **kwargs)	Continuous Triangular log-likelihood
Gumbel(name, *args, **kwargs)	Univariate Gumbel log-likelihood
Rice(name, *args, **kwargs)	Rice distribution.
Logistic(name, *args, **kwargs)	Logistic log-likelihood.
LogitNormal(name, *args, **kwargs)	Logit-Normal log-likelihood.
Interpolated(name, *args, **kwargs)	Univariate probability distribution defined as a linear interpolation of probability density function evaluated on some lattice of points.

A collection of common probability distributions for stochastic nodes in PyMC.

class pymc3.distributions.continuous.AsymmetricLaplace(name, *args, **kwargs)

Asymmetric-Laplace log-likelihood.

The pdf of this distribution is

\[\begin{split}{f(x|\\b,\kappa,\mu) = \left({\frac{\\b}{\kappa + 1/\kappa}}\right)\,e^{-(x-\mu)\\b\,s\kappa ^{s}}}\end{split}\]

where

\[s = sgn(x-\mu)\]

Support	\(x \in \mathbb{R}\)
Mean	\(\mu-\frac{\\\kappa-1/\kappa}b\)
Variance	\(\frac{1+\kappa^{4}}{b^2\kappa^2 }\)

Parameters

b: float

Scale parameter (b > 0)

kappa: float

Symmetry parameter (kappa > 0)

mu: float

Location parameter

See Also:

——–

`Reference <https://en.wikipedia.org/wiki/Asymmetric_Laplace_distribution>`_

logp(value)

Calculate log-probability of Asymmetric-Laplace distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random samples from this distribution, using the inverse CDF method.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size:int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Beta(name, *args, **kwargs)

Beta log-likelihood.

The pdf of this distribution is

\[f(x \mid \alpha, \beta) = \frac{x^{\alpha - 1} (1 - x)^{\beta - 1}}{B(\alpha, \beta)}\]

(Source code, png, hires.png, pdf)

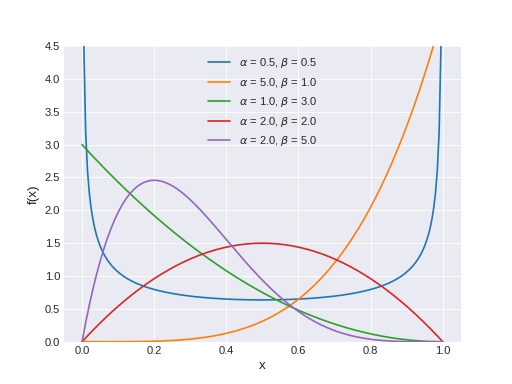
Support	\(x \in (0, 1)\)
Mean	\(\dfrac{\alpha}{\alpha + \beta}\)
Variance	\(\dfrac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\)

Beta distribution can be parameterized either in terms of alpha and beta or mean and standard deviation. The link between the two parametrizations is given by

\[ \begin{align}\begin{aligned}\begin{split}\alpha &= \mu \kappa \\ \beta &= (1 - \mu) \kappa\end{split}\\\text{where } \kappa = \frac{\mu(1-\mu)}{\sigma^2} - 1\end{aligned}\end{align} \]

Parameters

alpha: float

alpha > 0.

beta: float

beta > 0.

mu: float

Alternative mean (0 < mu < 1).

sigma: float

Alternative standard deviation (0 < sigma < sqrt(mu * (1 - mu))).

Notes

Beta distribution is a conjugate prior for the parameter \(p\) of the binomial distribution.

logcdf(value)

Compute the log of the cumulative distribution function for Beta distribution at the specified value.

Parameters

value: numeric

Value(s) for which log CDF is calculated.

Returns

TensorVariable

logp(value)

Calculate log-probability of Beta distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Beta distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Cauchy(name, *args, **kwargs)

Cauchy log-likelihood.

Also known as the Lorentz or the Breit-Wigner distribution.

The pdf of this distribution is

\[f(x \mid \alpha, \beta) = \frac{1}{\pi \beta [1 + (\frac{x-\alpha}{\beta})^2]}\]

(Source code, png, hires.png, pdf)

Support	\(x \in \mathbb{R}\)
Mode	\(\alpha\)
Mean	undefined
Variance	undefined

Parameters

alpha: float

Location parameter

beta: float

Scale parameter > 0

logcdf(value)

Compute the log of the cumulative distribution function for Cauchy distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Cauchy distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Cauchy distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.ChiSquared(name, *args, **kwargs)

\(\chi^2\) log-likelihood.

The pdf of this distribution is

\[f(x \mid \nu) = \frac{x^{(\nu-2)/2}e^{-x/2}}{2^{\nu/2}\Gamma(\nu/2)}\]

(Source code, png, hires.png, pdf)

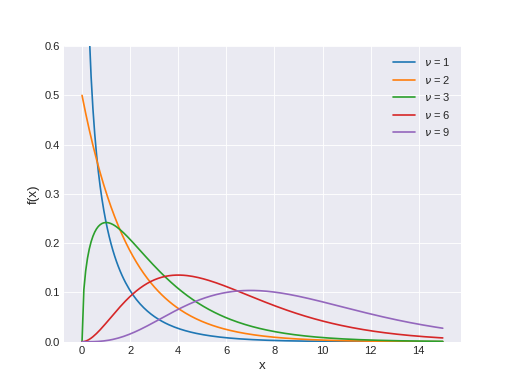
Support	\(x \in [0, \infty)\)
Mean	\(\nu\)
Variance	\(2 \nu\)

Parameters

nu: int

Degrees of freedom (nu > 0).

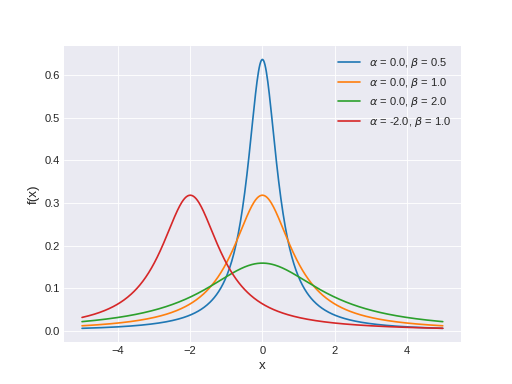
class pymc3.distributions.continuous.ExGaussian(name, *args, **kwargs)

Exponentially modified Gaussian log-likelihood.

Results from the convolution of a normal distribution with an exponential distribution.

The pdf of this distribution is

\[f(x \mid \mu, \sigma, \tau) = \frac{1}{\nu}\; \exp\left\{\frac{\mu-x}{\nu}+\frac{\sigma^2}{2\nu^2}\right\} \Phi\left(\frac{x-\mu}{\sigma}-\frac{\sigma}{\nu}\right)\]

where \(\Phi\) is the cumulative distribution function of the standard normal distribution.

(Source code, png, hires.png, pdf)

Support	\(x \in \mathbb{R}\)
Mean	\(\mu + \nu\)
Variance	\(\sigma^2 + \nu^2\)

Parameters

mu: float

Mean of the normal distribution.

sigma: float

Standard deviation of the normal distribution (sigma > 0).

nu: float

Mean of the exponential distribution (nu > 0).

References

Rigby2005

Rigby R.A. and Stasinopoulos D.M. (2005). “Generalized additive models for location, scale and shape” Applied Statististics., 54, part 3, pp 507-554.

Lacouture2008

Lacouture, Y. and Couseanou, D. (2008). “How to use MATLAB to fit the ex-Gaussian and other probability functions to a distribution of response times”. Tutorials in Quantitative Methods for Psychology, Vol. 4, No. 1, pp 35-45.

logcdf(value)

Compute the log of the cumulative distribution function for ExGaussian distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

References

Rigby2005

R.A. Rigby (2005). “Generalized additive models for location, scale and shape” https://doi.org/10.1111/j.1467-9876.2005.00510.x

logp(value)

Calculate log-probability of ExGaussian distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from ExGaussian distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Exponential(name, *args, **kwargs)

Exponential log-likelihood.

The pdf of this distribution is

\[f(x \mid \lambda) = \lambda \exp\left\{ -\lambda x \right\}\]

(Source code, png, hires.png, pdf)

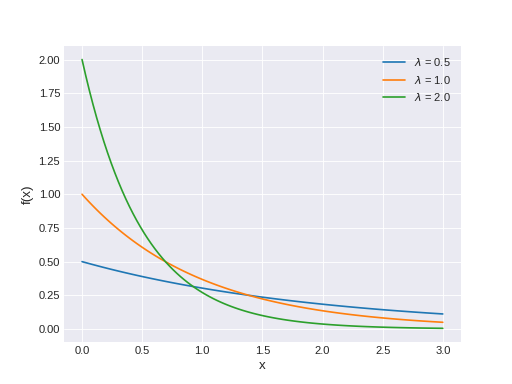
Support	\(x \in [0, \infty)\)
Mean	\(\dfrac{1}{\lambda}\)
Variance	\(\dfrac{1}{\lambda^2}\)

Parameters

lam: float

Rate or inverse scale (lam > 0)

logcdf(value)

Compute the log of cumulative distribution function for the Exponential distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Exponential distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Exponential distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Flat(name, *args, **kwargs)

Uninformative log-likelihood that returns 0 regardless of the passed value.

logcdf(value)

Compute the log of the cumulative distribution function for Flat distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Flat distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Raises ValueError as it is not possible to sample from Flat distribution

Parameters

point: dict, optional

size: int, optional

Raises

ValueError

class pymc3.distributions.continuous.Gamma(name, *args, **kwargs)

Gamma log-likelihood.

Represents the sum of alpha exponentially distributed random variables, each of which has mean beta.

The pdf of this distribution is

\[f(x \mid \alpha, \beta) = \frac{\beta^{\alpha}x^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)}\]

(Source code, png, hires.png, pdf)

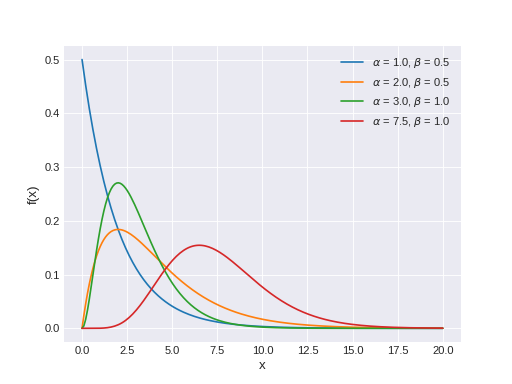
Support	\(x \in (0, \infty)\)
Mean	\(\dfrac{\alpha}{\beta}\)
Variance	\(\dfrac{\alpha}{\beta^2}\)

Gamma distribution can be parameterized either in terms of alpha and beta or mean and standard deviation. The link between the two parametrizations is given by

\[\begin{split}\alpha &= \frac{\mu^2}{\sigma^2} \\ \beta &= \frac{\mu}{\sigma^2}\end{split}\]

Parameters

alpha: float

Shape parameter (alpha > 0).

beta: float

Rate parameter (beta > 0).

mu: float

Alternative shape parameter (mu > 0).

sigma: float

Alternative scale parameter (sigma > 0).

logcdf(value)

Compute the log of the cumulative distribution function for Gamma distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Gamma distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Gamma distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Gumbel(name, *args, **kwargs)

Univariate Gumbel log-likelihood

The pdf of this distribution is

\[f(x \mid \mu, \beta) = \frac{1}{\beta}e^{-(z + e^{-z})}\]

where

\[z = \frac{x - \mu}{\beta}.\]

(Source code, png, hires.png, pdf)

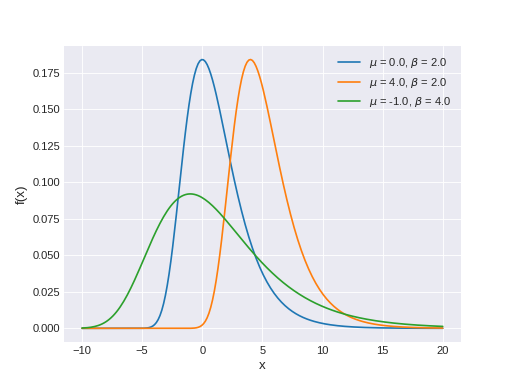
Support	\(x \in \mathbb{R}\)
Mean	\(\mu + \beta\gamma\), where \(\gamma\) is the Euler-Mascheroni constant
Variance	\(\frac{\pi^2}{6} \beta^2\)

Parameters

mu: float

Location parameter.

beta: float

Scale parameter (beta > 0).

logcdf(value)

Compute the log of the cumulative distribution function for Gumbel distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Gumbel distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Gumbel distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.HalfCauchy(name, *args, **kwargs)

Half-Cauchy log-likelihood.

The pdf of this distribution is

\[f(x \mid \beta) = \frac{2}{\pi \beta [1 + (\frac{x}{\beta})^2]}\]

(Source code, png, hires.png, pdf)

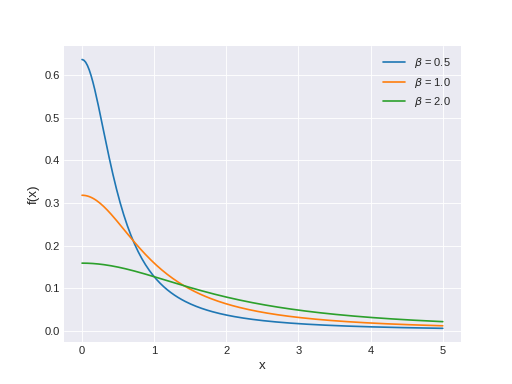
Support	\(x \in [0, \infty)\)
Mode	0
Mean	undefined
Variance	undefined

Parameters

beta: float

Scale parameter (beta > 0).

logcdf(value)

Compute the log of the cumulative distribution function for HalfCauchy distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of HalfCauchy distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from HalfCauchy distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.HalfFlat(name, *args, **kwargs)

Improper flat prior over the positive reals.

logcdf(value)

Compute the log of the cumulative distribution function for HalfFlat distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of HalfFlat distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Raises ValueError as it is not possible to sample from HalfFlat distribution

Parameters

point: dict, optional

size: int, optional

Raises

ValueError

class pymc3.distributions.continuous.HalfNormal(name, *args, **kwargs)

Half-normal log-likelihood.

The pdf of this distribution is

\[ \begin{align}\begin{aligned}f(x \mid \tau) = \sqrt{\frac{2\tau}{\pi}} \exp\left(\frac{-x^2 \tau}{2}\right)\\f(x \mid \sigma) = \sqrt{\frac{2}{\pi\sigma^2}} \exp\left(\frac{-x^2}{2\sigma^2}\right)\end{aligned}\end{align} \]

Note

The parameters sigma/tau (\(\sigma\)/\(\tau\)) refer to the standard deviation/precision of the unfolded normal distribution, for the standard deviation of the half-normal distribution, see below. For the half-normal, they are just two parameterisation \(\sigma^2 \equiv \frac{1}{\tau}\) of a scale parameter

(Source code, png, hires.png, pdf)

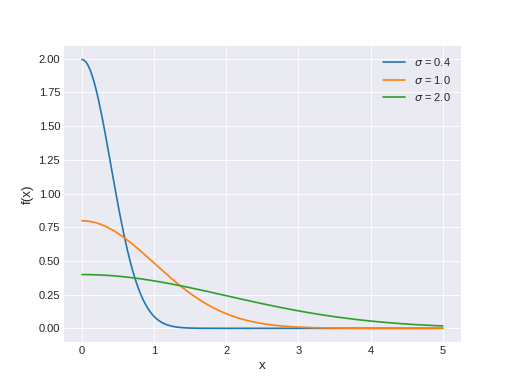
Support	\(x \in [0, \infty)\)
Mean	\(\sqrt{\dfrac{2}{\tau \pi}}\) or \(\dfrac{\sigma \sqrt{2}}{\sqrt{\pi}}\)
Variance	\(\dfrac{1}{\tau}\left(1 - \dfrac{2}{\pi}\right)\) or \(\sigma^2\left(1 - \dfrac{2}{\pi}\right)\)

Parameters

sigma: float

Scale parameter \(sigma\) (sigma > 0) (only required if tau is not specified).

tau: float

Precision \(tau\) (tau > 0) (only required if sigma is not specified).

Examples

with pm.Model():
    x = pm.HalfNormal('x', sigma=10)

with pm.Model():
    x = pm.HalfNormal('x', tau=1/15)

logcdf(value)

Compute the log of the cumulative distribution function for HalfNormal distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of HalfNormal distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from HalfNormal distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.HalfStudentT(name, *args, **kwargs)

Half Student’s T log-likelihood

The pdf of this distribution is

\[f(x \mid \sigma,\nu) = \frac{2\;\Gamma\left(\frac{\nu+1}{2}\right)} {\Gamma\left(\frac{\nu}{2}\right)\sqrt{\nu\pi\sigma^2}} \left(1+\frac{1}{\nu}\frac{x^2}{\sigma^2}\right)^{-\frac{\nu+1}{2}}\]

(Source code, png, hires.png, pdf)

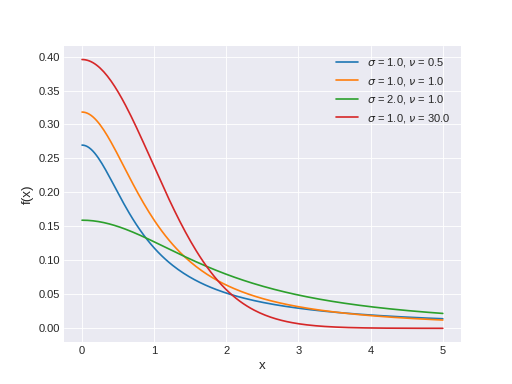
Support

\(x \in [0, \infty)\)

Parameters

nu: float

Degrees of freedom, also known as normality parameter (nu > 0).

sigma: float

Scale parameter (sigma > 0). Converges to the standard deviation as nu increases. (only required if lam is not specified)

lam: float

Scale parameter (lam > 0). Converges to the precision as nu increases. (only required if sigma is not specified)

Examples

# Only pass in one of lam or sigma, but not both.
with pm.Model():
    x = pm.HalfStudentT('x', sigma=10, nu=10)

with pm.Model():
    x = pm.HalfStudentT('x', lam=4, nu=10)

logp(value)

Calculate log-probability of HalfStudentT distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from HalfStudentT distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Interpolated(name, *args, **kwargs)

Univariate probability distribution defined as a linear interpolation of probability density function evaluated on some lattice of points.

The lattice can be uneven, so the steps between different points can have different size and it is possible to vary the precision between regions of the support.

The probability density function values don not have to be normalized, as the interpolated density is any way normalized to make the total probability equal to $1$.

Both parameters x_points and values pdf_points are not variables, but plain array-like objects, so they are constant and cannot be sampled.

Support

\(x \in [x\_points[0], x\_points[-1]]\)

Parameters

x_points: array-like

A monotonically growing list of values

pdf_points: array-like

Probability density function evaluated on lattice x_points

logp(value)

Calculate log-probability of Interpolated distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Interpolated distribution.

Parameters

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.InverseGamma(name, *args, **kwargs)

Inverse gamma log-likelihood, the reciprocal of the gamma distribution.

The pdf of this distribution is

\[f(x \mid \alpha, \beta) = \frac{\beta^{\alpha}}{\Gamma(\alpha)} x^{-\alpha - 1} \exp\left(\frac{-\beta}{x}\right)\]

(Source code, png, hires.png, pdf)

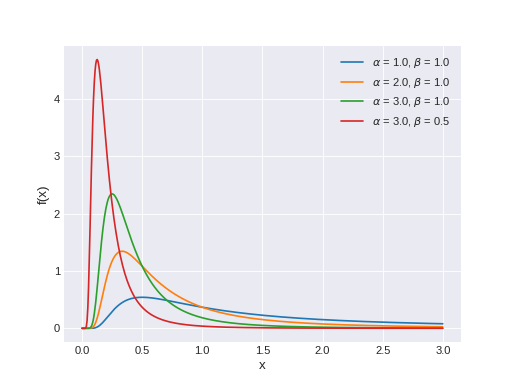
Support	\(x \in (0, \infty)\)
Mean	\(\dfrac{\beta}{\alpha-1}\) for \(\alpha > 1\)
Variance	\(\dfrac{\beta^2}{(\alpha-1)^2(\alpha - 2)}\) for \(\alpha > 2\)

Parameters

alpha: float

Shape parameter (alpha > 0).

beta: float

Scale parameter (beta > 0).

mu: float

Alternative shape parameter (mu > 0).

sigma: float

Alternative scale parameter (sigma > 0).

logcdf(value)

Compute the log of the cumulative distribution function for Inverse Gamma distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of InverseGamma distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from InverseGamma distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Kumaraswamy(name, *args, **kwargs)

Kumaraswamy log-likelihood.

The pdf of this distribution is

\[f(x \mid a, b) = abx^{a-1}(1-x^a)^{b-1}\]

(Source code, png, hires.png, pdf)

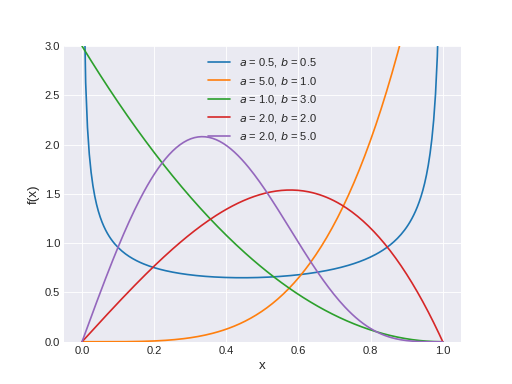
Support	\(x \in (0, 1)\)
Mean	\(b B(1 + \tfrac{1}{a}, b)\)
Variance	\(b B(1 + \tfrac{2}{a}, b) - (b B(1 + \tfrac{1}{a}, b))^2\)

Parameters

a: float

a > 0.

b: float

b > 0.

logp(value)

Calculate log-probability of Kumaraswamy distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Kumaraswamy distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Laplace(name, *args, **kwargs)

Laplace log-likelihood.

The pdf of this distribution is

\[f(x \mid \mu, b) = \frac{1}{2b} \exp \left\{ - \frac{|x - \mu|}{b} \right\}\]

(Source code, png, hires.png, pdf)

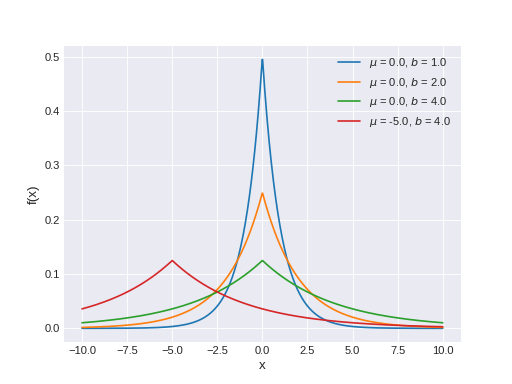
Support	\(x \in \mathbb{R}\)
Mean	\(\mu\)
Variance	\(2 b^2\)

Parameters

mu: float

Location parameter.

b: float

Scale parameter (b > 0).

logcdf(value)

Compute the log of the cumulative distribution function for Laplace distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Laplace distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Laplace distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Logistic(name, *args, **kwargs)

Logistic log-likelihood.

The pdf of this distribution is

\[f(x \mid \mu, s) = \frac{\exp\left(-\frac{x - \mu}{s}\right)}{s \left(1 + \exp\left(-\frac{x - \mu}{s}\right)\right)^2}\]

(Source code, png, hires.png, pdf)

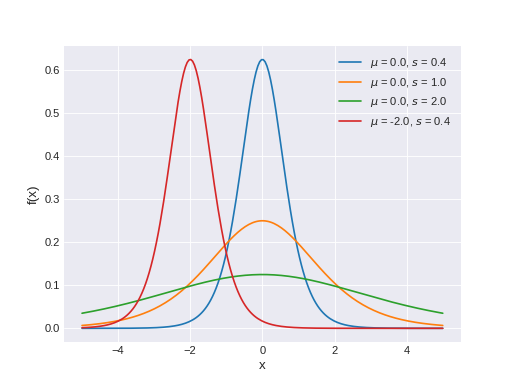
Support	\(x \in \mathbb{R}\)
Mean	\(\mu\)
Variance	\(\frac{s^2 \pi^2}{3}\)

Parameters

mu: float

Mean.

s: float

Scale (s > 0).

logcdf(value)

Compute the log of the cumulative distribution function for Logistic distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Logistic distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Logistic distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.LogitNormal(name, *args, **kwargs)

Logit-Normal log-likelihood.

The pdf of this distribution is

\[f(x \mid \mu, \tau) = \frac{1}{x(1-x)} \sqrt{\frac{\tau}{2\pi}} \exp\left\{ -\frac{\tau}{2} (logit(x)-\mu)^2 \right\}\]

(Source code, png, hires.png, pdf)

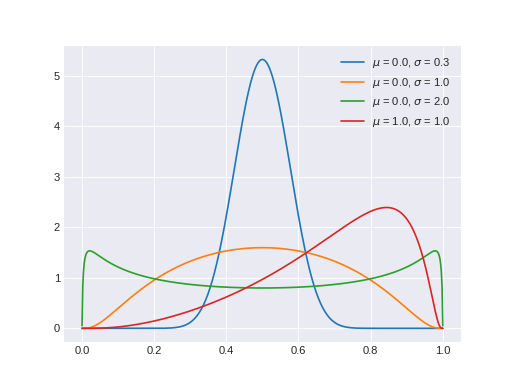
Support	\(x \in (0, 1)\)
Mean	no analytical solution
Variance	no analytical solution

Parameters

mu: float

Location parameter.

sigma: float

Scale parameter (sigma > 0).

tau: float

Scale parameter (tau > 0).

logp(value)

Calculate log-probability of LogitNormal distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from LogitNormal distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Lognormal(name, *args, **kwargs)

Log-normal log-likelihood.

Distribution of any random variable whose logarithm is normally distributed. A variable might be modeled as log-normal if it can be thought of as the multiplicative product of many small independent factors.

The pdf of this distribution is

\[f(x \mid \mu, \tau) = \frac{1}{x} \sqrt{\frac{\tau}{2\pi}} \exp\left\{ -\frac{\tau}{2} (\ln(x)-\mu)^2 \right\}\]

(Source code, png, hires.png, pdf)

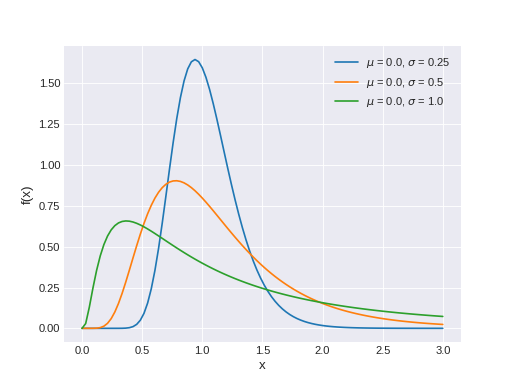
Support	\(x \in [0, \infty)\)
Mean	\(\exp\{\mu + \frac{1}{2\tau}\}\)
Variance	\((\exp\{\frac{1}{\tau}\} - 1) \times \exp\{2\mu + \frac{1}{\tau}\}\)

Parameters

mu: float

Location parameter.

sigma: float

Standard deviation. (sigma > 0). (only required if tau is not specified).

tau: float

Scale parameter (tau > 0). (only required if sigma is not specified).

Examples

# Example to show that we pass in only ``sigma`` or ``tau`` but not both.
with pm.Model():
    x = pm.Lognormal('x', mu=2, sigma=30)

with pm.Model():
    x = pm.Lognormal('x', mu=2, tau=1/100)

logcdf(value)

Compute the log of the cumulative distribution function for Lognormal distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Lognormal distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Lognormal distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Moyal(name, *args, **kwargs)

Moyal log-likelihood.

The pdf of this distribution is

\[f(x \mid \mu,\sigma) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\left(z + e^{-z}\right)},\]

where

\[z = \frac{x-\mu}{\sigma}.\]

(Source code, png, hires.png, pdf)

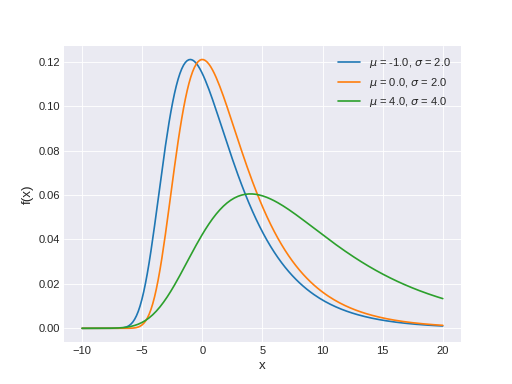
Support	\(x \in (-\infty, \infty)\)
Mean	\(\mu + \sigma\left(\gamma + \log 2\right)\), where \(\gamma\) is the Euler-Mascheroni constant
Variance	\(\frac{\pi^{2}}{2}\sigma^{2}\)

Parameters

mu: float

Location parameter.

sigma: float

Scale parameter (sigma > 0).

logcdf(value)

Compute the log of the cumulative distribution function for Moyal distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Moyal distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Moyal distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Normal(name, *args, **kwargs)

Univariate normal log-likelihood.

The pdf of this distribution is

\[f(x \mid \mu, \tau) = \sqrt{\frac{\tau}{2\pi}} \exp\left\{ -\frac{\tau}{2} (x-\mu)^2 \right\}\]

Normal distribution can be parameterized either in terms of precision or standard deviation. The link between the two parametrizations is given by

\[\tau = \dfrac{1}{\sigma^2}\]

(Source code, png, hires.png, pdf)

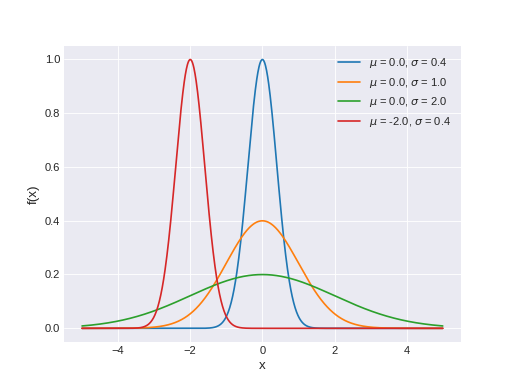
Support	\(x \in \mathbb{R}\)
Mean	\(\mu\)
Variance	\(\dfrac{1}{\tau}\) or \(\sigma^2\)

Parameters

mu: float

Mean.

sigma: float

Standard deviation (sigma > 0) (only required if tau is not specified).

tau: float

Precision (tau > 0) (only required if sigma is not specified).

Examples

with pm.Model():
    x = pm.Normal('x', mu=0, sigma=10)

with pm.Model():
    x = pm.Normal('x', mu=0, tau=1/23)

logcdf(value)

Compute the log of the cumulative distribution function for Normal distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Normal distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Normal distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Pareto(name, *args, **kwargs)

Pareto log-likelihood.

Often used to characterize wealth distribution, or other examples of the 80/20 rule.

The pdf of this distribution is

\[f(x \mid \alpha, m) = \frac{\alpha m^{\alpha}}{x^{\alpha+1}}\]

(Source code, png, hires.png, pdf)

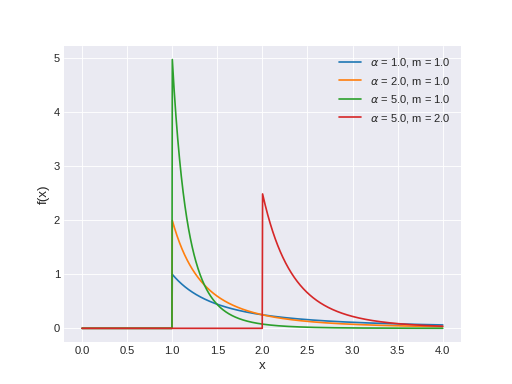
Support	\(x \in [m, \infty)\)
Mean	\(\dfrac{\alpha m}{\alpha - 1}\) for \(\alpha \ge 1\)
Variance	\(\dfrac{m \alpha}{(\alpha - 1)^2 (\alpha - 2)}\) for \(\alpha > 2\)

Parameters

alpha: float

Shape parameter (alpha > 0).

m: float

Scale parameter (m > 0).

logcdf(value)

Compute the log of the cumulative distribution function for Pareto distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Pareto distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Pareto distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Rice(name, *args, **kwargs)

Rice distribution.

\[f(x\mid \nu ,\sigma )= {\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right),\]

(Source code, png, hires.png, pdf)

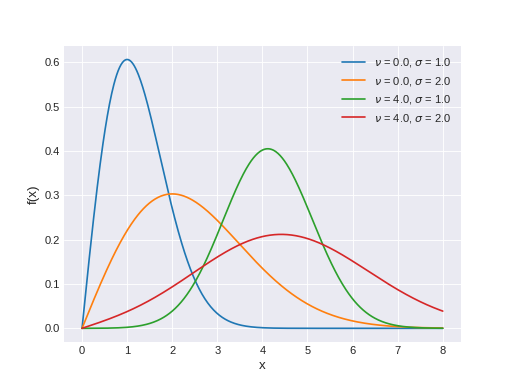
Support	\(x \in (0, \infty)\)
Mean	\(\sigma {\sqrt {\pi /2}}\,\,L_{{1/2}}(-\nu ^{2}/2\sigma ^{2})\)
Variance	\(2\sigma ^{2}+\nu ^{2}-{\frac {\pi \sigma ^{2}}{2}}L_{{1/2}}^{2}\left({\frac {-\nu ^{2}}{2\sigma ^{2}}}\right)\)

Parameters

nu: float

noncentrality parameter.

sigma: float

scale parameter.

b: float

shape parameter (alternative to nu).

Notes

The distribution \(\mathrm{Rice}\left(|\nu|,\sigma\right)\) is the distribution of \(R=\sqrt{X^2+Y^2}\) where \(X\sim N(\nu \cos{\theta}, \sigma^2)\), \(Y\sim N(\nu \sin{\theta}, \sigma^2)\) are independent and for any real \(\theta\).

The distribution is defined with either nu or b. The link between the two parametrizations is given by

\[b = \dfrac{\nu}{\sigma}\]

logp(value)

Calculate log-probability of Rice distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Rice distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.SkewNormal(name, *args, **kwargs)

Univariate skew-normal log-likelihood.

The pdf of this distribution is

\[f(x \mid \mu, \tau, \alpha) = 2 \Phi((x-\mu)\sqrt{\tau}\alpha) \phi(x,\mu,\tau)\]

(Source code, png, hires.png, pdf)

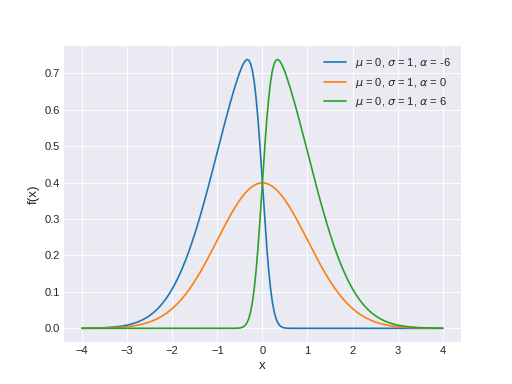
Support	\(x \in \mathbb{R}\)
Mean	\(\mu + \sigma \sqrt{\frac{2}{\pi}} \frac {\alpha }{{\sqrt {1+\alpha ^{2}}}}\)
Variance	\(\sigma^2 \left( 1-\frac{2\alpha^2}{(\alpha^2+1) \pi} \right)\)

Skew-normal distribution can be parameterized either in terms of precision or standard deviation. The link between the two parametrizations is given by

\[\tau = \dfrac{1}{\sigma^2}\]

Parameters

mu: float

Location parameter.

sigma: float

Scale parameter (sigma > 0).

tau: float

Alternative scale parameter (tau > 0).

alpha: float

Skewness parameter.

Notes

When alpha=0 we recover the Normal distribution and mu becomes the mean, tau the precision and sigma the standard deviation. In the limit of alpha approaching plus/minus infinite we get a half-normal distribution.

logp(value)

Calculate log-probability of SkewNormal distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from SkewNormal distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.StudentT(name, *args, **kwargs)

Student’s T log-likelihood.

Describes a normal variable whose precision is gamma distributed. If only nu parameter is passed, this specifies a standard (central) Student’s T.

The pdf of this distribution is

\[f(x|\mu,\lambda,\nu) = \frac{\Gamma(\frac{\nu + 1}{2})}{\Gamma(\frac{\nu}{2})} \left(\frac{\lambda}{\pi\nu}\right)^{\frac{1}{2}} \left[1+\frac{\lambda(x-\mu)^2}{\nu}\right]^{-\frac{\nu+1}{2}}\]

(Source code, png, hires.png, pdf)

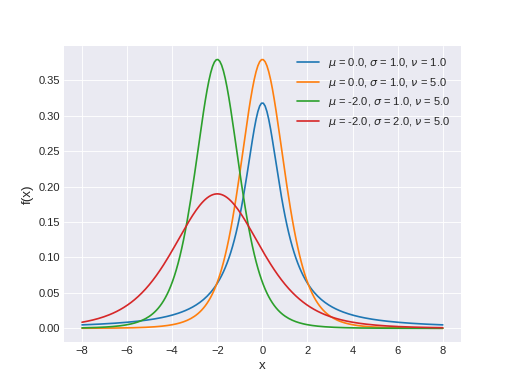
Support

\(x \in \mathbb{R}\)

Parameters

nu: float

Degrees of freedom, also known as normality parameter (nu > 0).

mu: float

Location parameter.

sigma: float

Scale parameter (sigma > 0). Converges to the standard deviation as nu increases. (only required if lam is not specified)

lam: float

Scale parameter (lam > 0). Converges to the precision as nu increases. (only required if sigma is not specified)

Examples

with pm.Model():
    x = pm.StudentT('x', nu=15, mu=0, sigma=10)

with pm.Model():
    x = pm.StudentT('x', nu=15, mu=0, lam=1/23)

logcdf(value)

Compute the log of the cumulative distribution function for Student’s T distribution at the specified value.

Parameters

value: numeric

Value(s) for which log CDF is calculated.

Returns

TensorVariable

logp(value)

Calculate log-probability of StudentT distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from StudentT distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Triangular(name, *args, **kwargs)

Continuous Triangular log-likelihood

The pdf of this distribution is

\[\begin{split}\begin{cases} 0 & \text{for } x < a, \\ \frac{2(x-a)}{(b-a)(c-a)} & \text{for } a \le x < c, \\[4pt] \frac{2}{b-a} & \text{for } x = c, \\[4pt] \frac{2(b-x)}{(b-a)(b-c)} & \text{for } c < x \le b, \\[4pt] 0 & \text{for } b < x. \end{cases}\end{split}\]

(Source code, png, hires.png, pdf)

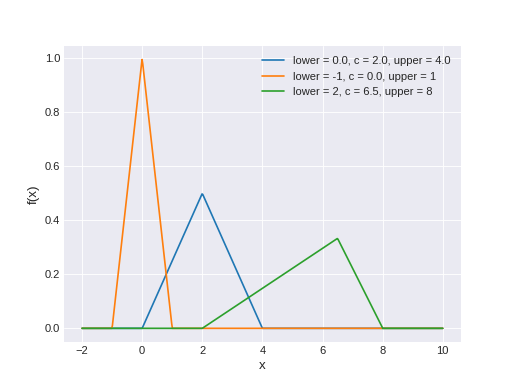
Support	\(x \in [lower, upper]\)
Mean	\(\dfrac{lower + upper + c}{3}\)
Variance	\(\dfrac{upper^2 + lower^2 +c^2 - lower*upper - lower*c - upper*c}{18}\)

Parameters

lower: float

Lower limit.

c: float

mode

upper: float

Upper limit.

logcdf(value)

Compute the log of the cumulative distribution function for Triangular distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Triangular distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Triangular distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.TruncatedNormal(name, *args, **kwargs)

Univariate truncated normal log-likelihood.

The pdf of this distribution is

\[f(x;\mu ,\sigma ,a,b)={\frac {\phi ({\frac {x-\mu }{\sigma }})}{ \sigma \left(\Phi ({\frac {b-\mu }{\sigma }})-\Phi ({\frac {a-\mu }{\sigma }})\right)}}\]

Truncated normal distribution can be parameterized either in terms of precision or standard deviation. The link between the two parametrizations is given by

\[\tau = \dfrac{1}{\sigma^2}\]

(Source code, png, hires.png, pdf)

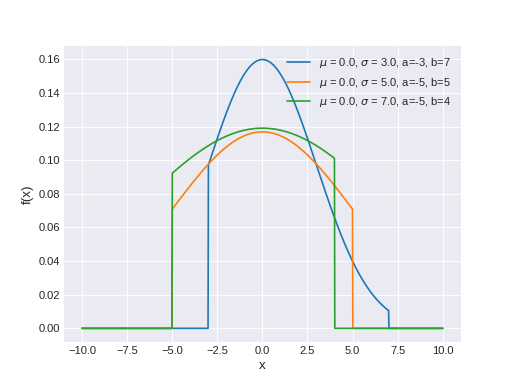
Support	\(x \in [a, b]\)
Mean	\(\mu +{\frac {\phi (\alpha )-\phi (\beta )}{Z}}\sigma\)
Variance	\(\sigma ^{2}\left[1+{\frac {\alpha \phi (\alpha )-\beta \phi (\beta )}{Z}}-\left({\frac {\phi (\alpha )-\phi (\beta )}{Z}}\right)^{2}\right]\)

Parameters

mu: float

Mean.

sigma: float

Standard deviation (sigma > 0).

lower: float (optional)

Left bound.

upper: float (optional)

Right bound.

Examples

with pm.Model():
    x = pm.TruncatedNormal('x', mu=0, sigma=10, lower=0)

with pm.Model():
    x = pm.TruncatedNormal('x', mu=0, sigma=10, upper=1)

with pm.Model():
    x = pm.TruncatedNormal('x', mu=0, sigma=10, lower=0, upper=1)

logp(value)

Calculate log-probability of TruncatedNormal distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from TruncatedNormal distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Uniform(name, *args, **kwargs)

Continuous uniform log-likelihood.

The pdf of this distribution is

\[f(x \mid lower, upper) = \frac{1}{upper-lower}\]

(Source code, png, hires.png, pdf)

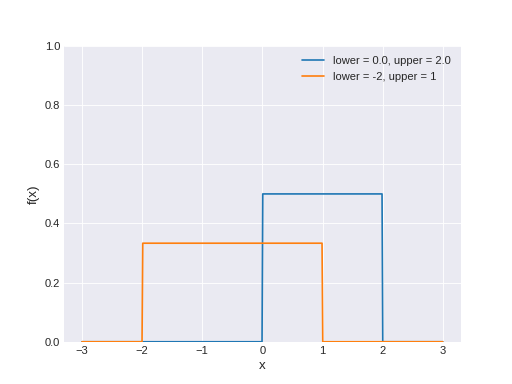
Support	\(x \in [lower, upper]\)
Mean	\(\dfrac{lower + upper}{2}\)
Variance	\(\dfrac{(upper - lower)^2}{12}\)

Parameters

lower: float

Lower limit.

upper: float

Upper limit.

logcdf(value)

Compute the log of the cumulative distribution function for Uniform distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Uniform distribution at specified value.

Parameters

value: numeric

Value for which log-probability is calculated.

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Uniform distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.VonMises(name, *args, **kwargs)

Univariate VonMises log-likelihood.

The pdf of this distribution is

\[f(x \mid \mu, \kappa) = \frac{e^{\kappa\cos(x-\mu)}}{2\pi I_0(\kappa)}\]

where \(I_0\) is the modified Bessel function of order 0.

(Source code, png, hires.png, pdf)

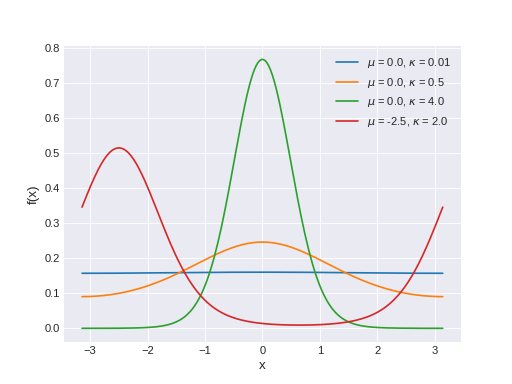
Support	\(x \in [-\pi, \pi]\)
Mean	\(\mu\)
Variance	\(1-\frac{I_1(\kappa)}{I_0(\kappa)}\)

Parameters

mu: float

Mean.

kappa: float

Concentration (frac{1}{kappa} is analogous to sigma^2).

logp(value)

Calculate log-probability of VonMises distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from VonMises distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Wald(name, *args, **kwargs)

Wald log-likelihood.

The pdf of this distribution is

\[f(x \mid \mu, \lambda) = \left(\frac{\lambda}{2\pi}\right)^{1/2} x^{-3/2} \exp\left\{ -\frac{\lambda}{2x}\left(\frac{x-\mu}{\mu}\right)^2 \right\}\]

(Source code, png, hires.png, pdf)

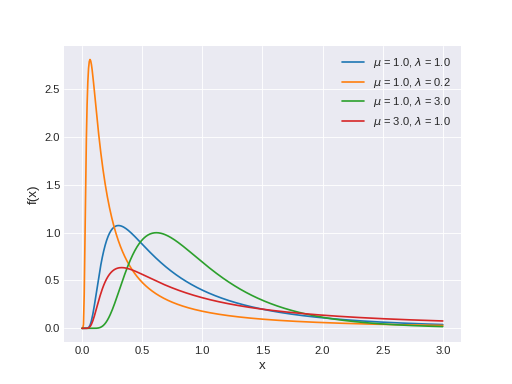
Support	\(x \in (0, \infty)\)
Mean	\(\mu\)
Variance	\(\dfrac{\mu^3}{\lambda}\)

Wald distribution can be parameterized either in terms of lam or phi. The link between the two parametrizations is given by

\[\phi = \dfrac{\lambda}{\mu}\]

Parameters

mu: float, optional

Mean of the distribution (mu > 0).

lam: float, optional

Relative precision (lam > 0).

phi: float, optional

Alternative shape parameter (phi > 0).

alpha: float, optional

Shift/location parameter (alpha >= 0).

Notes

To instantiate the distribution specify any of the following

• only mu (in this case lam will be 1)

• mu and lam

• mu and phi

• lam and phi

References

Tweedie1957

Tweedie, M. C. K. (1957). Statistical Properties of Inverse Gaussian Distributions I. The Annals of Mathematical Statistics, Vol. 28, No. 2, pp. 362-377

Michael1976

Michael, J. R., Schucany, W. R. and Hass, R. W. (1976). Generating Random Variates Using Transformations with Multiple Roots. The American Statistician, Vol. 30, No. 2, pp. 88-90

Giner2016

Göknur Giner, Gordon K. Smyth (2016) statmod: Probability Calculations for the Inverse Gaussian Distribution

logcdf(value)

Compute the log of the cumulative distribution function for Wald distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Wald distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Wald distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.continuous.Weibull(name, *args, **kwargs)

Weibull log-likelihood.

The pdf of this distribution is

\[f(x \mid \alpha, \beta) = \frac{\alpha x^{\alpha - 1} \exp(-(\frac{x}{\beta})^{\alpha})}{\beta^\alpha}\]

(Source code, png, hires.png, pdf)

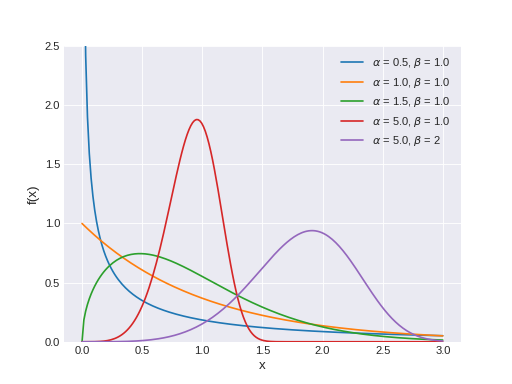
Support	\(x \in [0, \infty)\)
Mean	\(\beta \Gamma(1 + \frac{1}{\alpha})\)
Variance	\(\beta^2 \Gamma(1 + \frac{2}{\alpha} - \mu^2/\beta^2)\)

Parameters

alpha: float

Shape parameter (alpha > 0).

beta: float

Scale parameter (beta > 0).

logcdf(value)

Compute the log of the cumulative distribution function for Weibull distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor

Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)

Calculate log-probability of Weibull distribution at specified value.

Parameters

value: numeric

Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)

Draw random values from Weibull distribution.

Parameters

point: dict, optional

Dict of variable values on which random values are to be conditioned (uses default point if not specified).

size: int, optional

Desired size of random sample (returns one sample if not specified).

Returns

array