Discrete¶

`Binomial`(name, args, *kwargs)	Binomial log-likelihood.
`ZeroInflatedBinomial`(name, args, *kwargs)	Zero-inflated Binomial log-likelihood.
`BetaBinomial`(name, args, *kwargs)	Beta-binomial log-likelihood.
`Bernoulli`(name, args, *kwargs)	Bernoulli log-likelihood
`Poisson`(name, args, *kwargs)	Poisson log-likelihood.
`ZeroInflatedPoisson`(name, args, *kwargs)	Zero-inflated Poisson log-likelihood.
`NegativeBinomial`(name, args, *kwargs)	Negative binomial log-likelihood.
`ZeroInflatedNegativeBinomial`(name, *args, …)	Zero-Inflated Negative binomial log-likelihood.
`DiscreteUniform`(name, args, *kwargs)	Discrete uniform distribution.
`Geometric`(name, args, *kwargs)	Geometric log-likelihood.
`Categorical`(name, args, *kwargs)	Categorical log-likelihood.
`DiscreteWeibull`(name, args, *kwargs)	Discrete Weibull log-likelihood
`Constant`(name, args, *kwargs)	Constant log-likelihood.
`OrderedLogistic`(name, args, *kwargs)	Ordered Logistic log-likelihood.

class pymc3.distributions.discrete.Bernoulli(name, *args, **kwargs)¶

Bernoulli log-likelihood

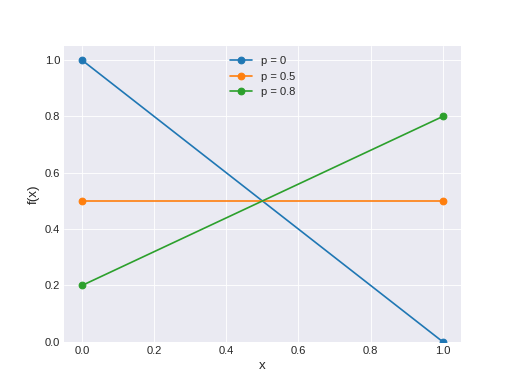
The Bernoulli distribution describes the probability of successes (x=1) and failures (x=0). The pmf of this distribution is

\[f(x \mid p) = p^{x} (1-p)^{1-x}\]

(Source code, png, hires.png, pdf)

Support	\(x \in \{0, 1\}\)
Mean	\(p\)
Variance	\(p (1 - p)\)

Parameters

p: float: Probability of success (0 < p < 1).
logit_p: float: Logit of success probability. Only one of p and logit_p can be specified.

logcdf(value)¶

Compute the log of the cumulative distribution function for Bernoulli distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor: Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of Bernoulli distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from Bernoulli distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.BetaBinomial(name, *args, **kwargs)¶

Beta-binomial log-likelihood.

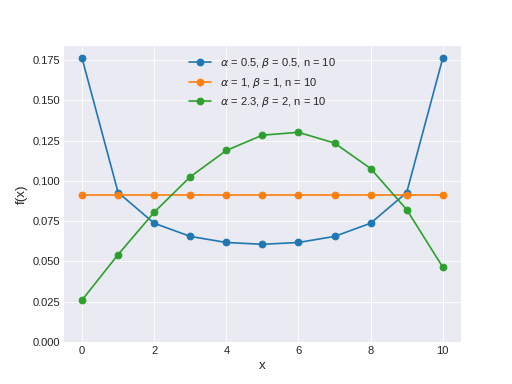
Equivalent to binomial random variable with success probability drawn from a beta distribution. The pmf of this distribution is

\[f(x \mid \alpha, \beta, n) = \binom{n}{x} \frac{B(x + \alpha, n - x + \beta)}{B(\alpha, \beta)}\]

(Source code, png, hires.png, pdf)

Support	\(x \in \{0, 1, \ldots, n\}\)
Mean	\(n \dfrac{\alpha}{\alpha + \beta}\)
Variance	\(n \dfrac{\alpha \beta}{(\alpha+\beta)^2 (\alpha+\beta+1)}\)

Parameters

n: int: Number of Bernoulli trials (n >= 0).
alpha: float: alpha > 0.
beta: float: beta > 0.

logcdf(value)¶

Compute the log of the cumulative distribution function for BetaBinomial distribution at the specified value.

Parameters

value: numeric: Value for which log CDF is calculated.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of BetaBinomial distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from BetaBinomial distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.Binomial(name, *args, **kwargs)¶

Binomial log-likelihood.

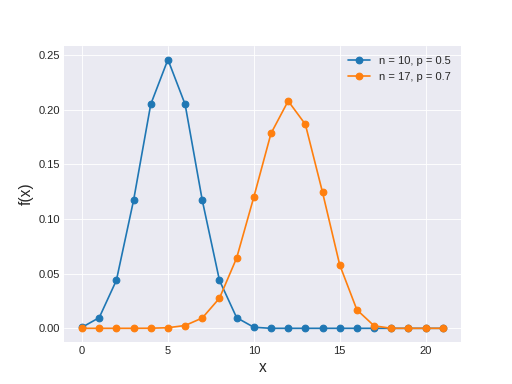
The discrete probability distribution of the number of successes in a sequence of n independent yes/no experiments, each of which yields success with probability p. The pmf of this distribution is

\[f(x \mid n, p) = \binom{n}{x} p^x (1-p)^{n-x}\]

(Source code, png, hires.png, pdf)

Support	\(x \in \{0, 1, \ldots, n\}\)
Mean	\(n p\)
Variance	\(n p (1 - p)\)

Parameters

n: int: Number of Bernoulli trials (n >= 0).
p: float: Probability of success in each trial (0 < p < 1).

logcdf(value)¶

Compute the log of the cumulative distribution function for Binomial distribution at the specified value.

Parameters

value: numeric: Value for which log CDF is calculated.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of Binomial distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from Binomial distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.Categorical(name, *args, **kwargs)¶

Categorical log-likelihood.

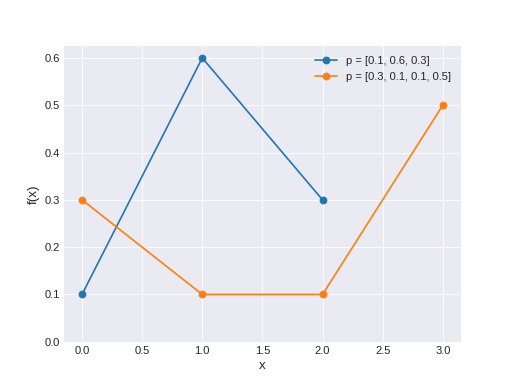
The most general discrete distribution. The pmf of this distribution is

\[f(x \mid p) = p_x\]

(Source code, png, hires.png, pdf)

Support

\(x \in \{0, 1, \ldots, |p|-1\}\)

Parameters

p: array of floats: p > 0 and the elements of p must sum to 1. They will be automatically rescaled otherwise.

logp(value)¶

Calculate log-probability of Categorical distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from Categorical distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.Constant(name, *args, **kwargs)¶

Constant log-likelihood.

Parameters

value: float or int: Constant parameter.

logp(value)¶

Calculate log-probability of Constant distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from Constant distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

pymc3.distributions.discrete.ConstantDist¶: alias of pymc3.distributions.discrete.Constant

class pymc3.distributions.discrete.DiscreteUniform(name, *args, **kwargs)¶

Discrete uniform distribution. The pmf of this distribution is

\[f(x \mid lower, upper) = \frac{1}{upper-lower+1}\]

(Source code, png, hires.png, pdf)

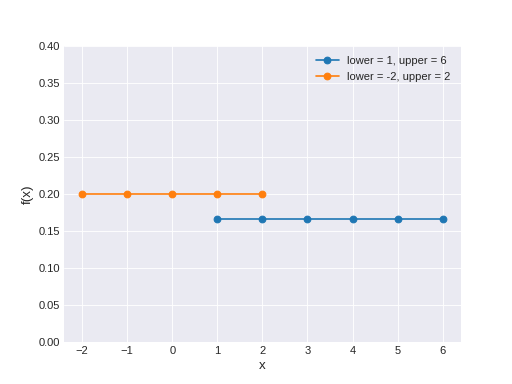
Support	\(x \in {lower, lower + 1, \ldots, upper}\)
Mean	\(\dfrac{lower + upper}{2}\)
Variance	\(\dfrac{(upper - lower)^2}{12}\)

Parameters

lower: int: Lower limit.
upper: int: Upper limit (upper > lower).

logcdf(value)¶

Compute the log of the cumulative distribution function for Discrete uniform distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor: Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of DiscreteUniform distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from DiscreteUniform distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.DiscreteWeibull(name, *args, **kwargs)¶

Discrete Weibull log-likelihood

The discrete Weibull distribution is a flexible model of count data that can handle both over- and under-dispersion. The pmf of this distribution is

\[f(x \mid q, \beta) = q^{x^{\beta}} - q^{(x + 1)^{\beta}}\]

(Source code, png, hires.png, pdf)

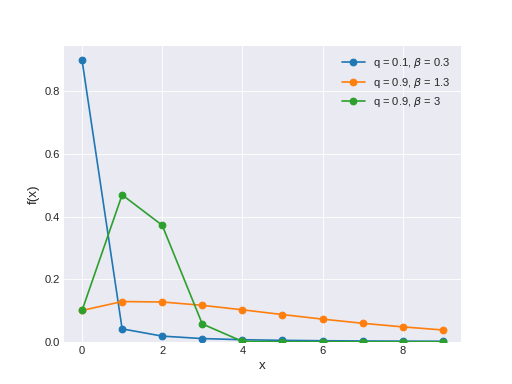
Support	\(x \in \mathbb{N}_0\)
Mean	\(\mu = \sum_{x = 1}^{\infty} q^{x^{\beta}}\)
Variance	\(2 \sum_{x = 1}^{\infty} x q^{x^{\beta}} - \mu - \mu^2\)

logcdf(value)¶

Compute the log of the cumulative distribution function for Discrete Weibull distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor: Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of DiscreteWeibull distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from DiscreteWeibull distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.Geometric(name, *args, **kwargs)¶

Geometric log-likelihood.

The probability that the first success in a sequence of Bernoulli trials occurs on the x’th trial. The pmf of this distribution is

\[f(x \mid p) = p(1-p)^{x-1}\]

(Source code, png, hires.png, pdf)

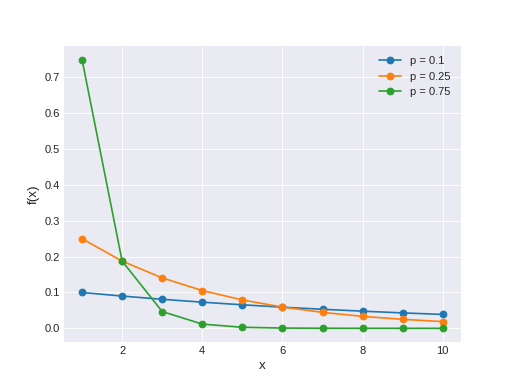
Support	\(x \in \mathbb{N}_{>0}\)
Mean	\(\dfrac{1}{p}\)
Variance	\(\dfrac{1 - p}{p^2}\)

Parameters

p: float: Probability of success on an individual trial (0 < p <= 1).

logcdf(value)¶

Compute the log of the cumulative distribution function for Geometric distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor: Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of Geometric distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from Geometric distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.HyperGeometric(name, *args, **kwargs)¶

Discrete hypergeometric distribution.

The probability of \(x\) successes in a sequence of \(n\) bernoulli trials taken without replacement from a population of \(N\) objects, containing \(k\) good (or successful or Type I) objects. The pmf of this distribution is

\[f(x \mid N, n, k) = \frac{\binom{k}{x}\binom{N-k}{n-x}}{\binom{N}{n}}\]

(Source code, png, hires.png, pdf)

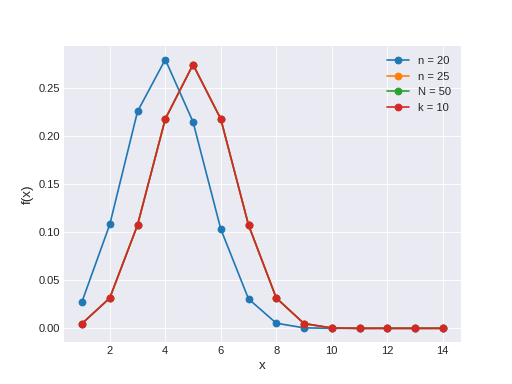
Support	\(x \in \left[\max(0, n - N + k), \min(k, n)\right]\)
Mean	\(\dfrac{nk}{N}\)
Variance	\(\dfrac{(N-n)nk(N-k)}{(N-1)N^2}\)

Parameters

Ninteger: Total size of the population
kinteger: Number of successful individuals in the population
ninteger: Number of samples drawn from the population

logcdf(value)¶

Compute the log of the cumulative distribution function for HyperGeometric distribution at the specified value.

Parameters

value: numeric: Value for which log CDF is calculated.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of HyperGeometric distribution at specified value.

Parameters

valuenumeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from HyperGeometric distribution.

Parameters

pointdict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
sizeint, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.NegativeBinomial(name, *args, **kwargs)¶

Negative binomial log-likelihood.

The negative binomial distribution describes a Poisson random variable whose rate parameter is gamma distributed. The pmf of this distribution is

\[f(x \mid \mu, \alpha) = \binom{x + \alpha - 1}{x} (\alpha/(\mu+\alpha))^\alpha (\mu/(\mu+\alpha))^x\]

(Source code, png, hires.png, pdf)

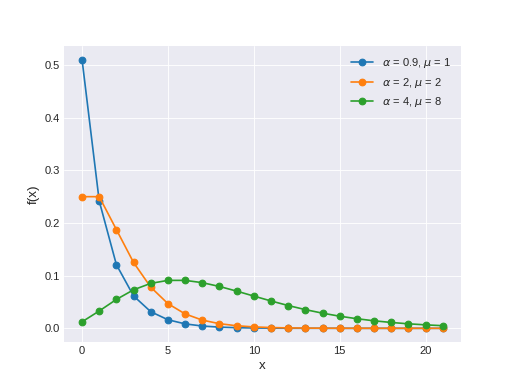
Support	\(x \in \mathbb{N}_0\)
Mean	\(\mu\)

The negative binomial distribution can be parametrized either in terms of mu or p, and either in terms of alpha or n. The link between the parametrizations is given by

\[\begin{split}\mu &= \frac{n(1-p)}{p} \\ \alpha &= n\end{split}\]

Parameters

mu: float: Poission distribution parameter (mu > 0).
alpha: float: Gamma distribution parameter (alpha > 0).
p: float: Alternative probability of success in each trial (0 < p < 1).
n: float: Alternative number of target success trials (n > 0)

logcdf(value)¶

Compute the log of the cumulative distribution function for NegativeBinomial distribution at the specified value.

Parameters

value: numeric: Value for which log CDF is calculated.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of NegativeBinomial distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from NegativeBinomial distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.OrderedLogistic(name, *args, **kwargs)¶

Ordered Logistic log-likelihood.

Useful for regression on ordinal data values whose values range from 1 to K as a function of some predictor, \(\eta\). The cutpoints, \(c\), separate which ranges of \(\eta\) are mapped to which of the K observed dependent variables. The number of cutpoints is K - 1. It is recommended that the cutpoints are constrained to be ordered.

\[\begin{split}f(k \mid \eta, c) = \left\{ \begin{array}{l} 1 - \text{logit}^{-1}(\eta - c_1) \,, \text{if } k = 0 \\ \text{logit}^{-1}(\eta - c_{k - 1}) - \text{logit}^{-1}(\eta - c_{k}) \,, \text{if } 0 < k < K \\ \text{logit}^{-1}(\eta - c_{K - 1}) \,, \text{if } k = K \\ \end{array} \right.\end{split}\]

Parameters

eta: float: The predictor.
c: array: The length K - 1 array of cutpoints which break \(\eta\) into ranges. Do not explicitly set the first and last elements of \(c\) to negative and positive infinity.

Examples

# Generate data for a simple 1 dimensional example problem
n1_c = 300; n2_c = 300; n3_c = 300
cluster1 = np.random.randn(n1_c) + -1
cluster2 = np.random.randn(n2_c) + 0
cluster3 = np.random.randn(n3_c) + 2

x = np.concatenate((cluster1, cluster2, cluster3))
y = np.concatenate((1*np.ones(n1_c),
                    2*np.ones(n2_c),
                    3*np.ones(n3_c))) - 1

# Ordered logistic regression
with pm.Model() as model:
    cutpoints = pm.Normal("cutpoints", mu=[-1,1], sigma=10, shape=2,
                          transform=pm.distributions.transforms.ordered)
    y_ = pm.OrderedLogistic("y", cutpoints=cutpoints, eta=x, observed=y)
    tr = pm.sample(1000)

# Plot the results
plt.hist(cluster1, 30, alpha=0.5);
plt.hist(cluster2, 30, alpha=0.5);
plt.hist(cluster3, 30, alpha=0.5);
plt.hist(tr["cutpoints"][:,0], 80, alpha=0.2, color='k');
plt.hist(tr["cutpoints"][:,1], 80, alpha=0.2, color='k');

class pymc3.distributions.discrete.Poisson(name, *args, **kwargs)¶

Poisson log-likelihood.

Often used to model the number of events occurring in a fixed period of time when the times at which events occur are independent. The pmf of this distribution is

\[f(x \mid \mu) = \frac{e^{-\mu}\mu^x}{x!}\]

(Source code, png, hires.png, pdf)

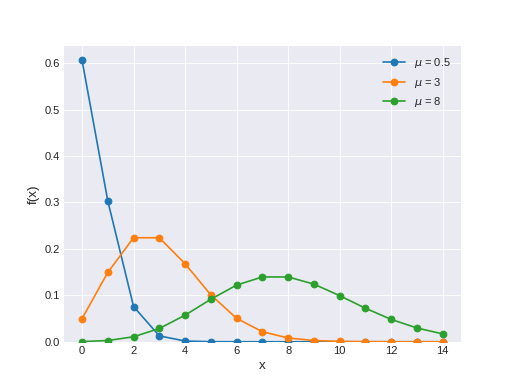
Support	\(x \in \mathbb{N}_0\)
Mean	\(\mu\)
Variance	\(\mu\)

Parameters

mu: float: Expected number of occurrences during the given interval (mu >= 0).

Notes

The Poisson distribution can be derived as a limiting case of the binomial distribution.

logcdf(value)¶

Compute the log of the cumulative distribution function for Poisson distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor: Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of Poisson distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from Poisson distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.ZeroInflatedBinomial(name, *args, **kwargs)¶

Zero-inflated Binomial log-likelihood.

The pmf of this distribution is

\[\begin{split}f(x \mid \psi, n, p) = \left\{ \begin{array}{l} (1-\psi) + \psi (1-p)^{n}, \text{if } x = 0 \\ \psi {n \choose x} p^x (1-p)^{n-x}, \text{if } x=1,2,3,\ldots,n \end{array} \right.\end{split}\]

(Source code, png, hires.png, pdf)

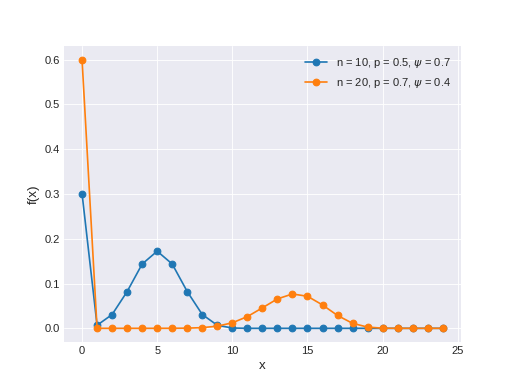
Support	\(x \in \mathbb{N}_0\)
Mean	\((1 - \psi) n p\)
Variance	\((1-\psi) n p [1 - p(1 - \psi n)].\)

Parameters

psi: float: Expected proportion of Binomial variates (0 < psi < 1)
n: int: Number of Bernoulli trials (n >= 0).
p: float: Probability of success in each trial (0 < p < 1).

logcdf(value)¶

Compute the log of the cumulative distribution function for ZeroInflatedBinomial distribution at the specified value.

Parameters

value: numeric: Value for which log CDF is calculated.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of ZeroInflatedBinomial distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from ZeroInflatedBinomial distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

class pymc3.distributions.discrete.ZeroInflatedNegativeBinomial(name, *args, **kwargs)¶

Zero-Inflated Negative binomial log-likelihood.

The Zero-inflated version of the Negative Binomial (NB). The NB distribution describes a Poisson random variable whose rate parameter is gamma distributed. The pmf of this distribution is

\[\begin{split}f(x \mid \psi, \mu, \alpha) = \left\{ \begin{array}{l} (1-\psi) + \psi \left ( \frac{\alpha}{\alpha+\mu} \right) ^\alpha, \text{if } x = 0 \\ \psi \frac{\Gamma(x+\alpha)}{x! \Gamma(\alpha)} \left ( \frac{\alpha}{\mu+\alpha} \right)^\alpha \left( \frac{\mu}{\mu+\alpha} \right)^x, \text{if } x=1,2,3,\ldots \end{array} \right.\end{split}\]

(Source code, png, hires.png, pdf)

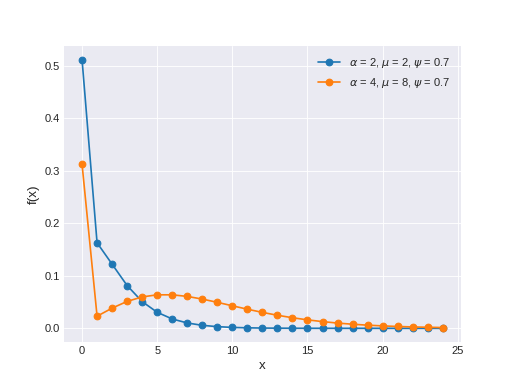
Support	\(x \in \mathbb{N}_0\)
Mean	\(\psi\mu\)
Var	\(\psi\mu + \left (1 + \frac{\mu}{\alpha} + \frac{1-\psi}{\mu} \right)\)

Parameters

psi: float: Expected proportion of NegativeBinomial variates (0 < psi < 1)
mu: float: Poission distribution parameter (mu > 0).
alpha: float: Gamma distribution parameter (alpha > 0).

logcdf(value)¶

Compute the log of the cumulative distribution function for ZeroInflatedNegativeBinomial distribution at the specified value.

Parameters

value: numeric: Value for which log CDF is calculated.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of ZeroInflatedNegativeBinomial distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from ZeroInflatedNegativeBinomial distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array

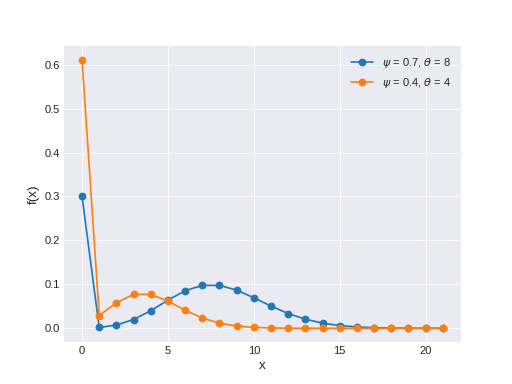
class pymc3.distributions.discrete.ZeroInflatedPoisson(name, *args, **kwargs)¶

Zero-inflated Poisson log-likelihood.

Often used to model the number of events occurring in a fixed period of time when the times at which events occur are independent. The pmf of this distribution is

\[\begin{split}f(x \mid \psi, \theta) = \left\{ \begin{array}{l} (1-\psi) + \psi e^{-\theta}, \text{if } x = 0 \\ \psi \frac{e^{-\theta}\theta^x}{x!}, \text{if } x=1,2,3,\ldots \end{array} \right.\end{split}\]

(Source code, png, hires.png, pdf)

Support	\(x \in \mathbb{N}_0\)
Mean	\(\psi\theta\)
Variance	\(\theta + \frac{1-\psi}{\psi}\theta^2\)

Parameters

psi: float: Expected proportion of Poisson variates (0 < psi < 1)
theta: float: Expected number of occurrences during the given interval (theta >= 0).

logcdf(value)¶

Compute the log of the cumulative distribution function for ZeroInflatedPoisson distribution at the specified value.

Parameters

value: numeric or np.ndarray or theano.tensor: Value(s) for which log CDF is calculated. If the log CDF for multiple values are desired the values must be provided in a numpy array or theano tensor.

Returns

TensorVariable

logp(value)¶

Calculate log-probability of ZeroInflatedPoisson distribution at specified value.

Parameters

value: numeric: Value(s) for which log-probability is calculated. If the log probabilities for multiple values are desired the values must be provided in a numpy array or theano tensor

Returns

TensorVariable

random(point=None, size=None)¶

Draw random values from ZeroInflatedPoisson distribution.

Parameters

point: dict, optional: Dict of variable values on which random values are to be conditioned (uses default point if not specified).
size: int, optional: Desired size of random sample (returns one sample if not specified).

Returns

array